Best Figure Counting Tricks for Triangles, Squares, and Cubes.
Best Figure Counting Tricks for Triangles, Squares, and Cubes.
With this trick, you can know the total number of triangles, squares and cubes from a figure and answer in 5seconds.
(1) Trick for triangle :-
 |
| (Figure–1) |
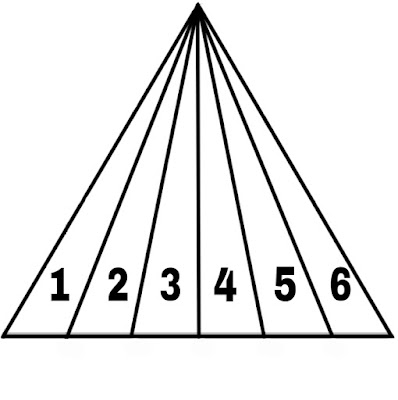
Now, we will know how to find the total number of triangles from a big triangle if it is divided into several smaller triangles.
If a triangle is divided into n numbers of smaller triangles (the size of each of the smaller triangles may or may not be equal here), then we have a trick to find the total number of triangles (N), i.e :-
N = 1 + 2 + 3 + 4 + .............. + n
Or, N = n(n+1)/2
Example–1
From Figure–1, n=3
The total number of triangles in Figure–1 (N) = 1 + 2 + 3 = 6
Or, N = 3(3+1)/2
= 3×4/2 = 6
Example–2
From Figure–2, n=6
The total number of triangles in the figure (N) = 1 + 2 + 3 + 4 + 5 + 6 = 21
Or, N = 6(6+1)/2
= 6×7/2 = 21
(2) Trick for square :-
 |
| (Figure–3) |
Here we will know how to find the number of total squares from a big square, if it is divided into several equal sizes of small squares.
If a square is divided into many equal sizes of small squares and has n number of small squares in a row, then we have a trick to find the total number of squares (N), i.e :-
N = 1² + 2² + 3² + 4² + ............... + n²
Or, N = n(n+1)(2n+1)/6
Example–1
From this figure, n=3, then
The total number of squares (N) = 1² + 2² +3² = 14
Or, N = 3(3+1)(2×3+1)/6
= 3×4×7/6 = 14
Example–2
From Figure-3, n=6, then
The total number of squares in Figure-3 (N) = 1² + 2² + 3² + 4² + 5² + 6² = 91
Or, N = 6(6+1)(2×6+1)/6
= 6×7×13/6 = 91
(3) Trick for cube :-
 |
| (Figure-5) |
Here we will know how to find out the total number of different cubes possible from a large cube, if it is divided into many equal sizes of small cubes.
If a cube is divided into many equal sizes of small cubes and contains n number of small cubes in a row, then we have a trick to find the total number of possible different cubes (N), i.e :-
N = 1³ + 2³ + 3³ + 4³ + .......... + n³
Or, N = {n(n+1)/2}²
Example–1
From Figure-5, n=2
Hence, the total number of possible cubes in Figure-5 (N) = 1³ + 2³ = 9
Or, N = {2(2+1)/2}²
= {2×3/2}² = {3}² = 9
Example–2
 |
| (Figure–6) |
From this figure, n=3
Hence the total number of possible cubes (N) = 1³ + 2³ + 3³ = 36
Or, N = {3(3+1)/2}²
= {3×4/2}² = {6}² = 36
(Q) –> A question for you, if we cut a big dice like figure-6, then how many small cubes do we get from this dice ? (Ans : 27)
Click here ⤵️





Comments